lastnamesong
[Coordinate] 회전, 회전변환행렬 (Rotation, Rotation Matrix) 본문
로봇의 움직임을 분석하고, 제어할 때 가장 기본이 되는 것이 "좌표계"에 대한 개념이다. 이는 로봇공학 뿐만 아니라 항공, 인체 동작 분석 등에서도 매우 중요한 개념이다. 예를 들어서 보행 로봇의 발끝이 한 발을 내딛을 때 우리는 로봇 발이 얼마만큼 어떤 방향으로 나아가야 하는지를 정의해주어야 한다. 로봇의 구동부는 각각을 기준으로 어떻게 회전, 병진운동 할지에 대한 제어가 가능하기 때문에, 우리는 각각의 움직임을 정의해주어야 한다. 이는 강화학습, 모델 기반 제어와 같은 상위단 제어 (high-level control)을 적용할 때에도 필요하다. 기준이 되는 좌표계를 잡고, 움직이는 파트 (e.g., 발 끝, 무릎 관절, 허벅지 프레임 등)에 새로운 좌표계를 정의하여 모든 분절에 대한 움직임을 정의할 수 있다. 이처럼 기본이 되는 좌표계의 표현, 변환을 위한 방법의 시작인 회전과 회전변환에 대해 다루고자 한다. 2차원, 3차원에서의 좌표를 다루기 때문에 벡터, 행렬의 연산을 포함한 선형대수학 관련 내용이 주로 다루어진다.
- Rotation
상대적으로 익숙한 2차원에서 좌표계 변환은 아래와 같이 정의될 수 있다.

2차원 좌표계 또는 벡터를 \( \theta \)만큼 회전 변환할 때의 회전변환행렬 (rotation matrix)는 \( \begin{bmatrix}cos\theta & -sin\theta \\sin\theta & cos\theta \end{bmatrix} \) 로 정의된다. 각도는 주로 반시계방향을 \( + \)으로 정의하며, 오른손 법칙을 떠올리면 수월하다. Rotation matrix는 시험을 준비할 때에는 암기의 대상이었다.
여기서 유심히 봐야하는 부분은 각도의 코사인과 사인을 unit vector (단위벡터)의 내적으로 표현할 수 있다는 점이다. 위 그림에서의 좌표계 변환이 정사영과 같은 것을 떠올릴 수 있으며, 벡터의 정사영에서는 내적이 사용된다. 이는 3차원에서도 같은 방법으로 적용이 가능하다.
여기에서 벡터와 행렬을 표현할 때 사용되는 notation (첨자)은 위 그림에서 설명되어있다시피, 우하단에는 표현하고자 하는 벡터나 변환, 우상단에는 그 기준이 되는 좌표계를 적었다. notation이나 unit vector를 표현하는 방식이 책이나 강의 자료마다 다른 경우가 있다 (e.g., unit vector를 \(i, j, k\)로 표현하거나, rotation matrix를 \( ^{0}R_{1}\) 등으로 표현). 그러므로 학업을 위해 이 글을 볼 때에는 주의하시기를..
3차원 회전변환도 같은 방식으로 정의할 수 있다.

이해를 돕기 위한 예시를 들어보면,

빨간색으로 저렇게 표시해두긴 했지만 결국 각 축방향 벡터를 정사영한 것이고 그 방법은 unit vector의 내적인 것이다.
수학에서는 차원을 확장해서 일반화할 수도 있겠지만, 로봇공학과 인체역학 분야에서의 회전 변환은 3차원 공간에서 이루어지므로 더 이상의 차원은 의미가 없다.
- Properties of Rotation Matrix
3차원 rotation matrix \( R = \begin{bmatrix}r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix}\)는 몇 가지 특징을 가지고 있다.
- 열벡터의 크기는 모두 1이다: \( \sqrt{r_{n1}^2 + r_{n2}^2 + r_{n3}^2} = 1, ( n\in \{1,2,3\} ) \)
- 각각의 열벡터는 서로 수직 (orthogonal)하다: \( \begin{pmatrix}r_{n1} \\ r_{n2} \\ r_{n3} \end{pmatrix} \cdot \begin{pmatrix}r_{m1} \\ r_{m2} \\ r_{m3} \end{pmatrix} = 0, (n,m \in \{1,2,3\}, n \neq m ) \)
위의 특징은 여섯 개의 constraints (제한 조건)이 되어 3차원 행렬의 아홉 개 변수 중 세 개 (\(9-6=3\))으로 rotation matrix를 정의할 수 있다. 물리적으로 생각해보면 3차원 회전을 3축에 대한 각도로 정의할 수 있으니 자명한 사실이다.
Orthogonal한 matrix \(Q\)는 \( Q^{T}Q = I\)라는 특성을 가지며, rotation matrix도 orthogonal하므로 이를 만족한다. 여기에 행렬식 (determinant)이 1이라는 특징을 추가로 가진다. Rotation matrix가 orthogonality를 만족하지만, orthogonal한 matrix가 모두 rotation matrix가 되는 것은 아니다.
$$ R^{T}R = I, det(R) = 1 \Leftrightarrow R \in SO(3)$$
여기서 처음으로 소개되는 것이 \(SO(3)\)이다. \(SO(n)\)은 n차원에서의 rotation matirx의 집합으로 정의된다. 여기서 \(SO\)는 special orthogonal의 줄임말이다. 이후에 보게 될 \(so\) (소문자)와는 다르므로 유의하자. (수학을 하거나 논문을 쓸 때에는 이런 정의가 중요하게 사용되므로 기억해두어야 한다.)
$$ SO(3) = \{ R \in \mathbb{R}^{3 \times3} | R^{T}R=I, det(R) = 1\} $$
Rotation matrix는 곱셈에 대해 몇 가지 특징을 가지고 있다. \(A, B, C \in SO(3)\)에 대해,
- \(AB \in SO(3) \): closed under multiplication
- \( (AB)C = A(BC) \): Associativity (결합법칙)
- \( ^{\exists} I \in SO(3), \) \( s.t. \) \( AI = IA = A\): identity element
- \( ^{\exists} A^{-1} \in SO(3), s.t., AA^{-1} = A^{-1}A = I\): inverse element
행렬의 곱셈에 대해 닫혀있기 때문에 역행렬, 단위행렬이 \(SO(3)\)에 속해있으며, 곱셈의 결합법칙 또한 성립한다.
그렇지만 교환법칙이 성립하지 않고 (\(AB \neq BA\)), 덧셈에 대해 닫혀있지 않다 (\(A+B \notin SO(3) \)). 때문에 \(SO(3)\)는 vector space가 될 수는 없다. Vector space에 대해서는 선형시스템에 대한 글을 작성할 때 소개될 수도 있으나 언제 쓰게 될지 모르므로.. https://en.wikipedia.org/wiki/Vector_space의 basis properties에서 소개하는 특징을 갖는 집합이구나 정도로 이해하면 좋을 것 같다.
Rotation matirx의 역행렬에 대해 간단하게 짚어보자면, 역행렬은 전치행렬 (transpose)과 같으며 (\( \because R^{T}R = I\)) 그 의미는 좌표계의 기준과 변환이 뒤집혔다고 생각할 수 있다.
$$ (R^{0}_1)^{-1} = (R^{0}_1)^{T} = R^{1}_0 $$
\( R^{0}_1 \) : orientation of frame 1 with respect to frame 0
\( R^{1}_0 \) : orientation of frame 0 with respect to frame 1
- Consecutive Rotations
위에서 설명했다시피, 3차원 rotation matrix는 곱셈의 교환법칙이 성립하지 않는다. 연속적인 회전변환에 대해서 2차원과 3차원으로 나누어 정리해보면 아래와 같다.

- Examples of Rotation Matrix
대표적으로 각 축 방향 별 회전 변환을 들 수 있으며, 다음 글에서 소개될 Euler angle, roll-pitch-yaw 이런 것들 모두 rotation matrix로 표현된다. 3차원에서의 x, y, z축에 대한 rotation matrix는 다음과 같다.
$$ Rot(x, \theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\theta & -sin\theta \\ 0 & sin\theta & cos\theta \end{bmatrix},$$ $$ Rot(y, \theta) = \begin{bmatrix} cos\theta & 0 & sin\theta \\ 0 & 1 & 0 \\ -sin\theta & 0 & cos\theta \end{bmatrix},$$
$$ Rot(z, \theta) = \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}.$$
이를 구하기 위해 계산기에 값을 일일이 넣어서 계산하는 사람은 없을 것이다. MATLAB에서는 rotx ,roty, rotz 함수를 통해 각 축에 대한 rotation matrix를 쉽게 구할 수 있다.

- Uses of Rotation Matrix
앞서 소개했던 것처럼 rotation matrix가 사용되는 방법은 크게 세 가지로 분류 가능하다.
- 어떤 좌표계를 다른 좌표계에서 표현할 때

- 어떤 벡터를 표현하기 위한 기준 좌표계를 바꿀 때
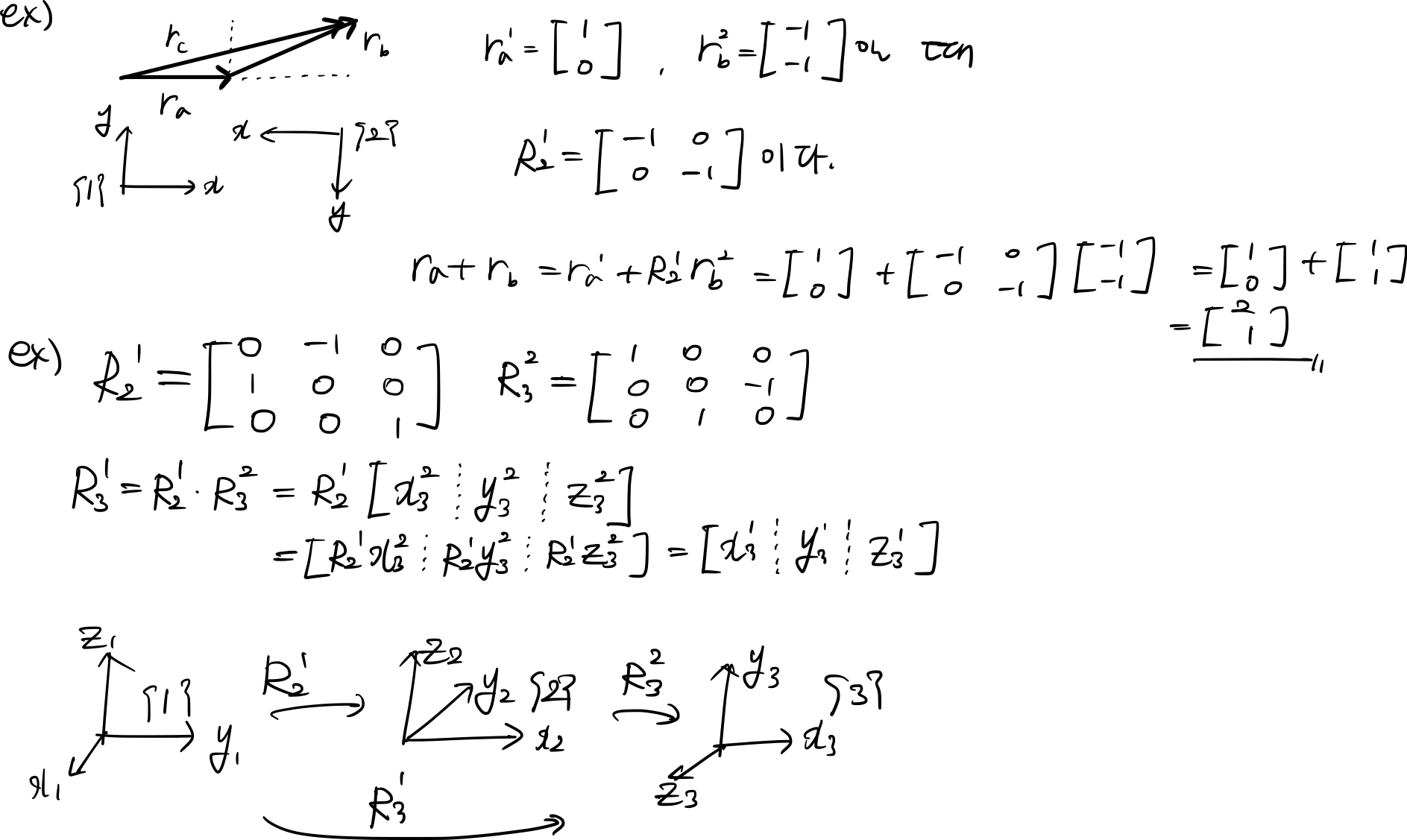
- 벡터에 대해 좌표계 변환을 할 때

Rotation matrix의 정의와 특성, 활용 방법 및 실제 MATLAB을 이용해 적용하는 방법에 대해 간단하게 알아보았다. 다음 글에서는 회전을 표현하기 위해 가장 많이 사용하는 방법 중 하나인 Euler angle (오일러 각)에 대해 알아보고 rotation matrix를 이용해 Euler angle을 정의하는 방법에 대해 정리할 것이다.
'Robotics > Geometry' 카테고리의 다른 글
| [Coordinate] Exponential Coordinates (0) | 2024.07.23 |
|---|---|
| [Rigid Body Motions] Body Twist (0) | 2024.07.19 |
| [Rigid Body Motions] Linear & Angular Velocities (0) | 2024.07.16 |
| [Transformation Matrices] Homogeneous Transformation (2) | 2023.10.15 |
| [Coordinate] 오일러 각 (Euler Angle) (1) | 2023.10.06 |