lastnamesong
[Rigid Body Motions] Body Twist 본문
[Rigid Body Motions] Linear & Angular Velocities
[Transformation Matrices] Homogeneous TransformationRotation의 경우 rotation matrix, Euler angle를 이용해 표현하는 방법에 대해 공부했다. 좌표계에서의 변환에서는 rotation (회전) 뿐만 아니라 translation (평행이동)
lastnamesong.tistory.com
이전 글에서는 rigid body의 linear velocity와 angular velocity에 대해 정리했고, rotation matrix를 이용해 skew-symmetric matrix를 만들고, 이를 이용해 angular velocity를 표현하는 방법을 소개했다.
Homogeneous transformation matrix에 대해서도 비슷한 방법으로 속도를 벡터로 표현할 수 있으며 그렇게 표현되는 벡터를 body twist, 또는 spatial velocity in the body frame 라고 한다. 이번 글에서는 이 body twist에 대해 정리한다.
- Background of Body Twist
우리는 \( dot(R) \)에 \(R^{-1}\)을 각각 앞과 뒤에 곱해줌으로써 angular velocity의 skew-symmetric matrix가 구해짐을 알고 있다. 비슷하게 homogeneous transformation matrix \( (T=\begin{bmatrix} R & r \\ 0 & 1 \end{bmatrix}) \)에 대해서도 \( \dot{T} \, \)에 \( T^{-1} \, \)을 곱하는 것을 고려해볼 수 있다.
$$ T^{-1}\dot{T} = \begin{bmatrix} R^{T} & -R^{T}r \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \dot{R} & \dot{r} \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} R^{T}\dot{R} & R^{T}\dot{r} \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} \hat{\omega}_{b} & v_b \\ 0 & 0 \end{bmatrix} $$
여기서 body twist가 정의된다. (논문에 따라 \( \omega_b\)와 \(v_b\)의 순서를 다르게 정의하는 경우도 있다. 수학적으로 푸는 데에는 문제가 없으나, 이후에 정의되는 operator와 transformation 등에서 약간의 차이가 있을 수 있으니 감안해서 읽어주시길...)
$$ V_b = \begin{bmatrix} \omega_b\\ v_b \end{bmatrix} \in \mathbb{R}^{6}$$
\(R^{T}\dot{R} \in so(3) \)이듯이, \( T^{-1}\dot{T} \)의 집합은 \( se(3) \)로 정의되며, \( V_b \)와 \( T^{-1}\dot{T} \)도 hat과 vee operator로 mapping이 가능하다.
$$ (T^{-1}\dot{T})^{\vee} = V_b, \: \hat{V_b} = T^{-1}\dot{T} $$
반대로 \(T^{-1}\)이 뒤에 곱해지는 경우에 대해서 정리해보면 아래와 같다.
$$ \dot{T}T^{-1} = \begin{bmatrix} \dot{R} & \dot{r} \\ 0 & 0 \end{bmatrix} \begin{bmatrix} R^{T} & -R^{T}r \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} \dot{R}R^T & \dot{r} - \dot{R}R^{T}r \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} \hat{\omega}_{s} & v_s \\ 0 & 0 \end{bmatrix} $$
\( \omega_s \)는 angular velocity 벡터를 \( \{s\} \) 기준으로 회전한 것이다. 그런데 \( v_s \)를 보면, 그리 단순해 보이지 않는다. 이 \(v_s \)는 fixed-frame ( \( \{s\} \)를 의미함)에서의 body-frame의 linear velocity가 아니다. 교과서에서도 \( v_s \)의 옳은 값은 \( \dot{r} \)라고 설명한다.
$$ v_s = \dot{r} - \dot{R}R^{T}r = \dot{r} - \hat{\omega}_{s}r$$
여기서 hat operator는 외적을 나타내므로 \( v_s = \dot{r} - \hat{\omega}_{s}r = \dot{r} + \omega_{s} \times (-r) \)가 된다.
Fixed-frame \( \{s\} \)의 원점이 움직인다는 것이 와닿지 않을 수 있지만,, 아래 그림의 initial configuration에서 \( \{s\} \)의 원점과 일치하는 가상의 점이라고 생각을 하면 이해가 될듯 하다.
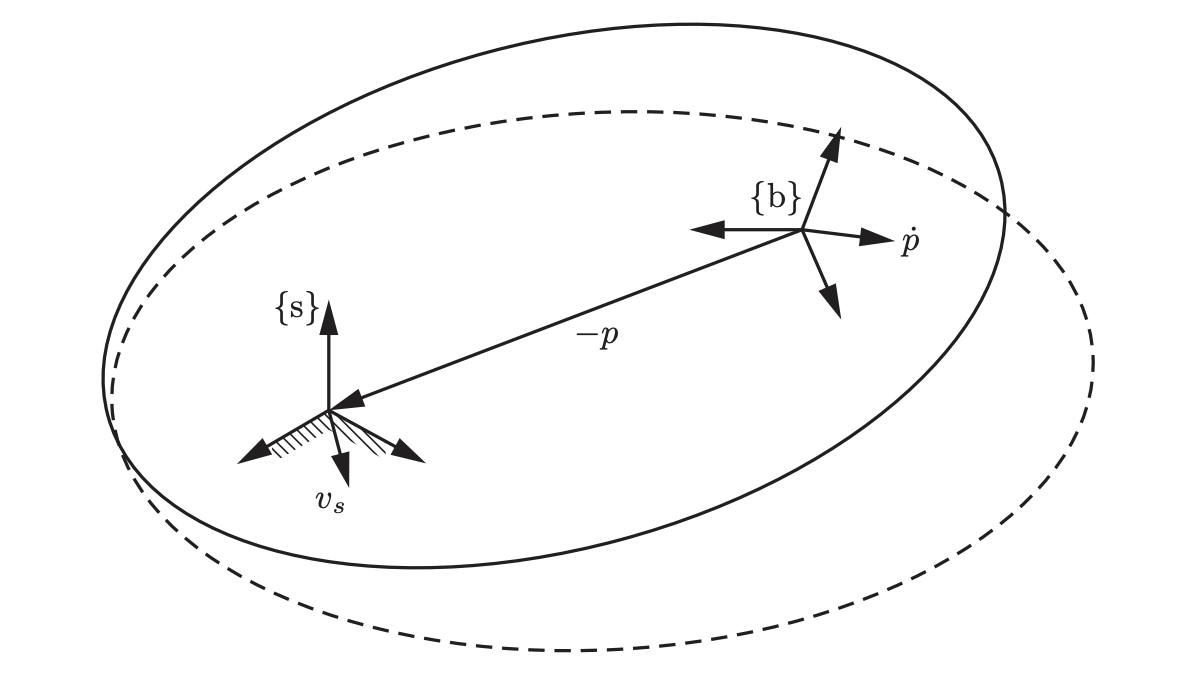
교과서에서는 body twist와 유사하게 \( V_s = \begin{bmatrix} \hat{\omega}_{s} \\ v_s \end{bmatrix} \)를 spatial velocity in the space frame, 또는 spatial twist라고 정의한다.
정의한 body twist와 spatial twist를 이용하여 아래와 같은 관계를 도출할 수 있다.
$$ \hat{V}_b = T^{-1}\dot{T} = T^{-1}\hat{V}_{s}T $$
반대로 \( \hat{V}_s = T\hat{V}_{b}T^{-1} \)로 쓸 수도 있고, transformation에 \(\begin{bmatrix} R & r \\ 0 & 1 \end{bmatrix} \)를 넣고 이전 글에서 증명하고 지지고 볶고 했던 hat operator 성질을 사용해서 곱셈을 계산하면 spatial twist를 아래와 같이 쓸 수 있다.
$$ \hat{V}_s = \begin{bmatrix} R\hat{\omega}_{b}R^{T} & -R\hat{\omega}_{b}R^{T}r + Rv_{b} \\ 0 & 0 \end{bmatrix}$$
여기에 vee operator를 쓰면 다음과 같은 식을 쓸 수 있다.
$$ \begin{bmatrix} \omega_{s} \\ v_s \end{bmatrix} = \begin{bmatrix} R & 0 \\ \hat{r}R & R \end{bmatrix} \begin{bmatrix} \omega_{b} \\ v_b \end{bmatrix} $$
- Adjoint Representation
여기서 body twist에 곱해지는 저 \( 6 \times 6 \) matrix를 새롭게 정의하게 된다. 이를 adjoint representation (또는 adjoint transformation)이라고 하며, 앞서 언급했던 것처럼 body twist를 정의할 때 linear / angular velocity의 순서가 달라지면 adjoint transformation도 정의가 달라지게 되므로 유의하자. (\( T=\begin{bmatrix} R \\r \end{bmatrix} \in SE(3) \)는 변함 없다. )
$$ Ad_{T} = \begin{bmatrix} R & 0 \\ \hat{r}R & R \end{bmatrix} \in \mathbb{R}^{6 \times 6} $$
자료에 따라서 adjoint mapping을 다양하게 표기한다.
$$ V^{'} = [Ad_T] V \quad or \quad V^{'} = Ad_T(V)$$
좌표계가 여러 개일 때에는 그 좌표계를 활용하기도 한다.
$$ Ad_{T^{A}_{B}} = Ad^{A}_{B}$$
\(SO(3)\), \( SE(3) \)와 유사하게, adjoint transformation도 몇 가지 특징을 갖는다. (\( T_1, T_2, T^{A}_{B}, T^{B}_{C} \in SE(3), \; V = \begin{bmatrix} \omega \\ v \end{bmatrix} \))
- \( Ad^{A}_{B}Ad^{B}_{C} = Ad^{A}_{C} \quad or \quad Ad_{T_1}(Ad_{T_2}(V)) = Ad_{T_{1}T_{2}}(V)\)
- \( (Ad^{A}_{B})^{-1} = Ad^{B}_{A} \quad or \quad [Ad_T]^{-1} = [Ad_{T^{-1}}] \)
- Examples Using Body Twists & Adjoint Transformation
아래 그림과 같은 수중 로봇이 있다고 가정해보자.
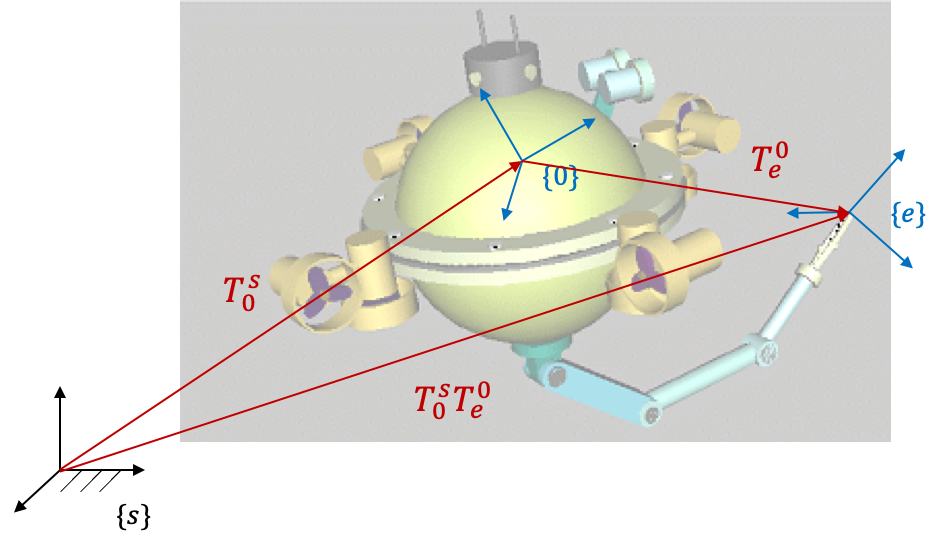
End-effector의 제어를 위해 fixed frame에 대한 end-effector의 속도를 알아야 하는 상황이다. 이를 위해 \( T^{-1}\dot{T} \, \)를 풀어보자.
$$ \hat{V}_e = (T^{s}_{e})^{-1} \frac{d}{dt}T^{s}_{e} = (T^{s}_{0}T^{0}_{e})^{-1}\frac{d}{dt}(T^{s}_{0}T^{0}_{e}) $$
여기서 \( (T^{s}_{0}T^{0}_{e})^{-1}\dfrac{d}{dt}(T^{s}_{0}T^{0}_{e}) = (T^{0}_{e})^{-1}(T^{s}_{0})^{-1}\left( \dot{T}^{s}_{0}T^{0}_{e} + T^{s}_{0}\dot{T}^{0}_{e} \right) = (T^{0}_{e})^{-1}\left( (T^{s}_{0})^{-1}\dot{T}^{s}_{0}\right)T^{0}_{e} + (T^{0}_{e})^{-1}\dot{T}^{0}_{e} \)로 정리할 수 있다. 그러면 우리가 잘 아는 twist와 homogeneous transformation matrix가 보인다.
$$ (T^{0}_{e})^{-1}\hat{V}_{0}T^{0}_{e} + \hat{V}_{e/0} = \begin{bmatrix} (R^{0}_{e})^T & -(R^{0}_{e})^{T}r^{0}_{e} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \hat{\omega}^{s}_{0} & v^{s}_{0} \\ 0 & 0 \end{bmatrix} \begin{bmatrix} R^{0}_{e} & r^{0}_{e} \\ 0 & 1 \end{bmatrix} + \hat{V}_{e/0} = \begin{bmatrix} (R^{0}_{e})^{T}\hat{\omega}^{s}_{0}R^{0}_{e} & (R^{0}_{e})^{T}\hat{\omega}^{s}_{0}r^{0}_{e} + (R^{0}_{e})^{T}v^{s}_{0} \\ 0 & 0 \end{bmatrix} + \hat{V}_{e/0}$$
앞서 hat operator의 성질을 사용해서 지지고 볶는다고 설명했던 그 부분을 적용하면,
\( \hat{a}b = a \times b \,\)에 의해 \( \hat{\omega}^{s}_{0}r^{0}_{e} = {\omega}^{s}_{0} \times r^{0}_{e} = - r^{0}_{e} \times {\omega}^{s}_{0} = - \hat{r}^{0}_{e} {\omega}^{s}_{0} \, \)이고, \( \widehat{Ra} = R\hat{a}R^T \)에 의해 \( (R^{0}_{e})^{T}\hat{\omega}^{s}_{0}R^{0}_{e} = \left( {(R^{0}_{e})^{T}\omega^{s}_{0}} \right)^{\wedge} \) 가 된다.
이를 종합하면,
$$ \hat{V}_e = \begin{bmatrix} \left( {(R^{0}_{e})^{T}\omega^{s}_{0}} \right)^{\wedge} & -(R^{0}_{e})^{T}\hat{r}^{0}_{e} {\omega}^{s}_{0 + (R^{0}_{e})^{T}v^{s}_{0}} \\ 0 & 0 \end{bmatrix} + \hat{V}_{e/0}$$
여기에 vee operator (\( \wedge \))를 적용하면,
$$ V_{e} \,(=V^{s}_{e})= \begin{bmatrix} -(R^{0}_{e})^{T}\hat{r}^{0}_{e}\omega^{s}_{0} + (R^{0}_{e})^Tv^{s}_{0} \\ (R^{0}_{e})^{T}\omega^{s}_{0} \end{bmatrix} + V_{e/0} =\begin{bmatrix} (R^{0}_{e})^T & 0 \\ -(R^{0}_{e})^T\hat{r}^{0}_{e} & (R^{0}_{e})^T \end{bmatrix} \begin{bmatrix} \omega^{s}_{0} \\ v^{s}_{0} \end{bmatrix} + V_{e/0}$$
\(.\begin{bmatrix} (R^{0}_{e})^T & 0 \\ -(R^{0}_{e})^T\hat{r}^{0}_{e} & (R^{0}_{e})^T \end{bmatrix} \)는 \( (Ad^{0}_{e})^{-1} = Ad^{e}_{0} \)이고, \( \begin{bmatrix} \omega^{s}_{0} \\ v^{s}_{0} \end{bmatrix} \)는 \( V_{0/s} \), 즉 로봇 body의twist이다.
body 좌표계에서 측정한 body의 velocity는 IMU와 같은 센서를 이용해서 측정이 가능하고, body frame에 대한 end-effector의 velocity는 forward kinematics를 이용하여 계산이 가능하다. 이로 인해 floating body 로봇에 대해, reference frame에서의 end-effector의 속도를 계산할 수 있다.
고백하자면 body twist 내용을 실제 로봇에 적용해본 적은 없다.. 그래서 그런가 이 글을 쓰기 위해 이전에 학습했던 내용들을 더 열심히 들여다본 것 같다. 이번에 내용을 정리하면서 로봇 시스템에 무언가 해보고 싶다는 생각이 조금 생기는 것 같기도 하다.
무엇이 부족해서 이런 생각들을 실천하지 못했던 것인가 하는 생각도 든다 ㅋㅋ
'Robotics > Geometry' 카테고리의 다른 글
| [Coordinate] Quaternion (쿼터니언, 사원수) (0) | 2024.07.26 |
|---|---|
| [Coordinate] Exponential Coordinates (0) | 2024.07.23 |
| [Rigid Body Motions] Linear & Angular Velocities (0) | 2024.07.16 |
| [Transformation Matrices] Homogeneous Transformation (2) | 2023.10.15 |
| [Coordinate] 오일러 각 (Euler Angle) (1) | 2023.10.06 |