lastnamesong
[옵션 거래] 블랙-숄즈 모형 (Black-Scholes Model) 본문
이전 글에서 옵션에 대해 개념적인 정리를 했다.
[경제금융용어 700선] 콜옵션, 풋옵션 (파생 상품)
어제 VIX에 관한 글을 쓰면서 VIX를 계산할 때 사용되는 콜옵션과 풋옵션 가격이 언급되었다. [경제금융용어 700선] VIX (공포지수, CBOE Volatility Index)월요일 (2024.08.05)에 코스피와 코스닥이 미친 듯
lastnamesong.tistory.com
위 글에서 든 예시에서는 옵션의 가격을 임의대로 정한 상태에서 설명을 했었다.
실제 시장에서는 옵션의 가격을 정하는 수식이 존재하며, 이에 대한 근간이 되는 모델인 블랙-숄즈 모델에 대해 정리해본다.
- Black-Scholes-Merton Model
블랙-숄즈 모형, 또는 블랙-숄즈-머튼 모형으로 정의되는 이 공식은 금용 시장에서 옵션의 가격을 계산하기 위한 수학적 모델이다. 이를 기반으로 콜옵션과 풋옵션의 가격이 결정되며 풋-콜 패리티와 같은 콜옵션과 풋옵션 사이의 관계에 대한 수식도 정의된다.
이를 정의하기에 앞서 수학적 모델이기 때문에 중요한 가정이 필요하다.
- 기초자산의 가격은 로그 정규 분포를 따른다: 주식의 로그 수익률은 정규 분포를 따르며, 이는 시간이 지남에 따라 주식 가격이 연속적으로 변동함을 의미한다.
- 무위험 이자율: 이자율은 일정하며 변하지 않는다.
- 옵션은 유럽형이다: 옵션은 만기일에만 행사할 수 있다.
- 배당금이 없다: 주식은 배당금을 지급하지 않는다.
- 시장 효율성: 시장은 효율적이며, 기회 비용이 없다.
- 거래 비용이 없다: 거래 시 발생하는 비용이 없다.
이런 가정이 가능한 배경은 "옵션의 가격이 올바르게 매겨진다면, 투자자가 옵션과 롱/숏 포지션을 조합하여 무위험으로 확실한 이익을 얻는 것이 불가능하다"는 철학에서 시작한다.
아무튼 이런 가정으로 정의되는 블랙-숄즈 모형은 아래와 같다.
$$ \frac{\partial V}{\partial t} + \dfrac{1}{2} {\sigma}^2S^2 \dfrac{\partial^2 V}{\partial S^2} + rS\dfrac{\partial V}{\partial S} - rV = 0 $$
\( V \)는 옵션의 가격, \( t \)는 시간, \( \sigma \)는 변동성, \( S \)는 기초자산의 가격, \( r \)은 무위험 이자율이다.
식이 복잡하긴 하지만 세부적인 내용보다는 그 가정과 배경에 대해 이해하고 대한 논리적인 타당성을 평가할 줄 아는 것이 더 중요하다고 생각한다.
- 콜옵션의 가격 계산
콜옵션 \( C \)의 가격은 기초자산의 가격 (\( S \))과 시간 (\( t \))의 함수로 정의될 수 있으며, 그 식은 아래와 같다.
$$ C(S,t) = N(d_1)S - Xe^{-r(T-t)}N(d_2) $$
여기서 \( X \)는 옵션의 행사가격, \( T \)는 옵션 만기일, \( N(\cdot) \)은 표준정규분포의 누적 분포 함수이며, \(d_1\)과 \(d_2\)는 다음과 같이 정의된다.
$$ \begin{matrix} d_1 = \dfrac{ln(\dfrac{S}{X})+(r+\dfrac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}} \\[5pt] d_2 = d_1 - \sigma\sqrt{T-t} \end{matrix} $$
- 풋옵션의 계산
풋옵션 \( P \)의 가격도 마찬가지로 기초자산의 가격 (\( S \))과 시간 (\( t \))의 함수로 정의될 수 있으며, 그 식은 아래와 같다.
$$ P(S,t) = Xe^{-r(T-t)} - S + C(S,t) = N(-d_2)Xe^{-r(T-t)}-N(-d_1)S $$
풋옵션의 경우, 가격이 하락할 때 수익을 얻는 특성으로 인해 계산이 상대적으로 더 복잡하다. 그래서 보통 풋-콜 패리티 (Put-Call Parity)라는 풋옵션과 콜옵션 사이의 관계를 이용할 수 있기 때문에 보통 콜옵션을 계산하고 풋-콜 패리티를 이용해 풋옵션을 계산하여 위와 같은 식이 나오게 되었다.
- 블랙-숄즈 모형의 의미
블랙-숄즈 모형은 옵션 가격 책정의 표준이 되었으며, 금융 시장에서 광범위하게 사용되고 있다. 이 모형의 도입으로 파생상품 시장이 급격히 성장했으며, 옵션 트레이딩 전략 및 리스크 관리 기법 개발에 큰 기여를 했습니다.
그러나 실제 시장은 모델에서 제시한 가정과 다른 경우가 많으므로 이 모형은 한계를 갖는다. 예를 들어, 모형은 주식 가격이 로그 정규 분포를 따른다고 가정하지만 실제 시장에서는 비정상적 가격 변동이나 폭락이 종종 발생한다. 또한, 모형은 배당금 지급, 변동성의 변화, 거래 비용 등 현실적인 요소를 고려하지 않기 때문에 많은 부분이 생략된 결과를 얻을 수 있다.
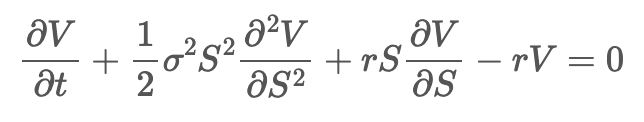
블랙-숄즈 모형은 옵션 가격 책정의 혁신적 도구로서, 금융공학의 발전에 중대한 영향을 주었다. 이 모형은 옵션 가격을 정확하게 계산할 수 있도록 도와주며, 시장 참여자들이 리스크를 관리하고 더 나은 투자 결정을 내릴 수 있는 기준이 된다. 하지만, 모형의 가정과 현실의 차이점을 이해하고, 필요할 때 보완적인 접근법을 사용하는 것이 중요하다.
더욱 학술적인 내용은 google scholar에서 black-scholes model로 검색하면 구체적이고 다양한 연구 내용을 찾을 수 있을 것이다.
'Life > Finance' 카테고리의 다른 글
| [옵션 거래] 커버드콜 (Covered Call, 고배당 ETF) (0) | 2024.08.19 |
|---|---|
| [옵션 거래] 풋-콜 패리티 (Put-Call Parity) (0) | 2024.08.16 |
| [경제금융용어 700선] 콜옵션, 풋옵션 (파생 상품) (0) | 2024.08.08 |
| [경제금융용어 700선] VIX (공포지수, CBOE Volatility Index) (0) | 2024.08.07 |
| [경제금융용어 700선] 뮤추얼펀드 (0) | 2024.08.06 |




