lastnamesong
[Coordinate] Quaternion (쿼터니언, 사원수) 본문
지금까지 정리했던 rotation matrix, Euler angle과 같은 표현 방법의 한계점이 분명히 존재한다.
가장 대표적인 문제는 Gimbal lock이며, 오일러 각으로 표현하는 세 축이 서로 독립적이지 않기 때문에 축이 겹쳐서 자유도를 잃는 상황이 발생하는 것이다. 이런 현상이 시스템을 제어할 때 일어나면 쉽지 않을 것이다.
또다른 문제로는 연산량의 문제이다. Rotation matrix를 이용하여 회전을 계산할 때에는 행렬 계산이 들어가게 되며, 이는 컴퓨터에서 계산할 때에 리소스 사용을 키우는 원인이 된다. 시뮬레이션 상황이라면 컴퓨터 성능을 높이면 되겠지만 모바일한 로봇의 연산장치로 이 행렬 계산을 매 제어 주기마다 계산하는 것은 현실적이지 못하다.
이의 대안으로 사용되는 것이 quaternion이며, 많이들 알고 있는 Unity, OpenGL과 같은 시뮬레이션 툴도 이 쿼터니언을 이용하여 위치를 표현한다.
이번 글에서는 쿼터니언의 정의와 성질, rotation matrix나 Euler angle과 quaternion 사이의 변환 방법에 대해 정리해본다.
- Definition of Quaternion
쿼터니언은 해석하면 사원수로, 복소수를 확장해서 만든 수 체계이다. 표현 방법의 일환으로 시작되었다. 네 개의 실수 성분을 가지며, 덧셈과 곱셈의 결합법칙 및 덧셈의 교환법칙을 만족시키지만 곱셈의 교환법칙은 성립하지 않는다.
수학적인 표현 방법은 다음과 같다.
$$ q = \langle w, x, y, z\rangle = w + x\mathbf{i} + y\mathbf{j} + z\mathbf{k} $$
\( \mathbf{i}, \mathbf{j}, \mathbf{k} \)는 사원수의 벡터 부분에 대한 basis (기저)이다. 사원수의 기저는 \( \{1, \mathbf{i}, \mathbf{j}, \mathbf{k} \} \)로 정의된다.
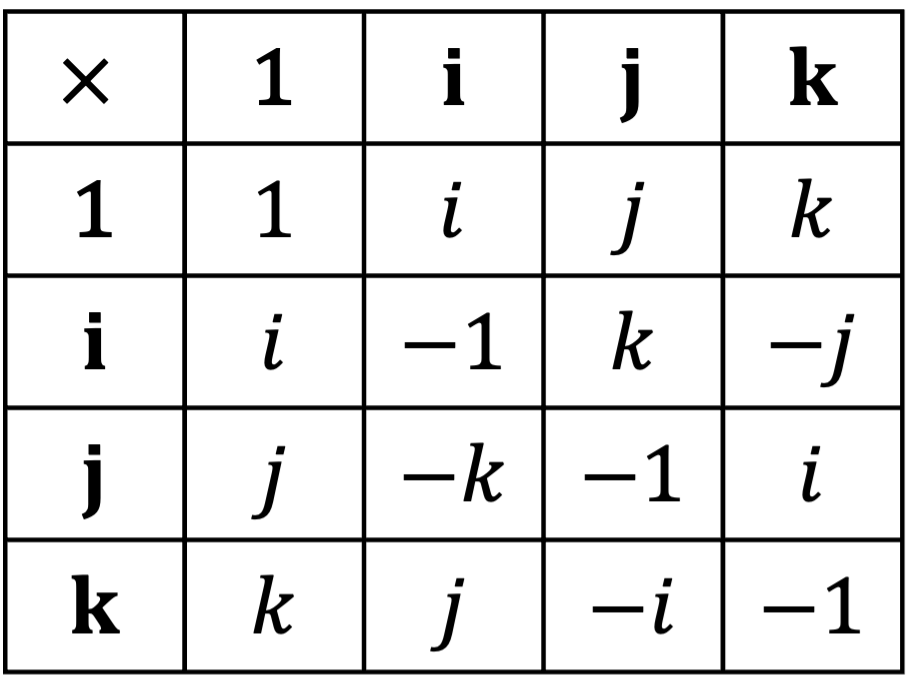
\( q = \langle w, x, y, z\rangle = w + x\mathbf{i} + y\mathbf{j} + z\mathbf{k} \)의 \( w \)는 \(q\)의 실수부로 정의하며 \( x\mathbf{i} + y\mathbf{j} + z\mathbf{k} \)는 \(q\)의 허수부라고 한다.
- Properties of Quaternion
정의에서 설명했듯 덧셈의 교환법칙과 결합법칙, 분배법칙이 성립하며 그 외의 성질은 아래와 같다.
- Scalar multiplication: \(nq = nw + nx\mathbf{i} + ny\mathbf{j} + nz\mathbf{k} \)
- Quaternion conjugate: Quaternion의 conjugate는 \( conj(q) = q{'} = w - x\mathbf{i} - y\mathbf{j} - z\mathbf{k} \)로 정의되며, 복소수의 complex conjugate과 유사한 것을 확인할 수 있다. $$ qa' * qb' = (qb*qa)' , \: q * q' = w^2 +x^2 + y^2 +z^2 $$
- Norm of quaternion: \( ||q||_2 = \sqrt{qq'} = \sqrt{w^2 + x^2 + y^2 +z^2} \)
- Inner/outer product: \( q_1 = \langle s_1, \vec{v}_1 \rangle, \: q_2 = \langle s_2, \vec{v}_2 \rangle,\)로 정의될 때,
$$ \begin{matrix} q_1 \cdot q_2 = s_1s_2 + \vec{v}_1 \cdot \vec{v}_2 \\ q_1 \times q_2 = \langle s_1s_2 - \vec{v}_1 \cdot \vec{v}_2, \; s_1\vec{v}_1 + s_2\vec{v}_2 + \vec{v}_1 \times \vec{v}_2\rangle \end{matrix}$$
- Inverse of quaternion: \( q^{-1} = \dfrac{q'}{q^2} \)
- Unit quaternion (identity quaternion): Identity 성분으로써의 성질을 만족해야하기 때문에 identity quaternion은 \( \langle 1, 0, 0, 0 \rangle \)로 정의된다.
- Quaternion to \( SO(3) \)
Quaternion \( q = \langle w, x, y, z\rangle \)를 rotation matrix로 변환하는 수식은 다음과 같다.
$$ R(q) = \begin{bmatrix} 2(w^2 + x^2)-1 & 2(xy-wz) & 2(zx+wy) \\ 2(xy+wz) & 2(w^2 + y^2)-1 & 2(yz - wx) \\ 2(zx - wy) & 2(yz + wx) & 2(w^2 + z^2)-1 \end{bmatrix}$$
오일러각 \( \Lambda = (\phi, \theta, \psi) \)로 쿼터니언을 계산하는 방법은 다음과 같다. 이때 오일러각은 ZYX (i.e., Roll-Pitch-Yaw)를 따른다.
$$ q = Q(\Lambda) = Q_Z(\psi)Q_y(\theta)Q_x(\phi) = \begin{bmatrix} cos(\frac{\psi}{2})cos(\frac{\theta}{2})cos(\frac{\phi}{2}) + sin(\frac{\psi}{2})sin(\frac{\theta}{2})sin(\frac{\phi}{2}) \\ cos(\frac{\psi}{2})cos(\frac{\theta}{2})sin(\frac{\phi}{2}) - sin(\frac{\psi}{2})sin(\frac{\theta}{2})cos(\frac{\phi}{2}) \\ cos(\frac{\psi}{2})sin(\frac{\theta}{2})cos(\frac{\phi}{2}) + sin(\frac{\psi}{2})cos(\frac{\theta}{2})sin(\frac{\phi}{2}) \\ sin(\frac{\psi}{2})cos(\frac{\theta}{2})cos(\frac{\phi}{2}) - cos(\frac{\psi}{2})sin(\frac{\theta}{2})sin(\frac{\phi}{2}) \end{bmatrix} $$
여기서 각 축 별 쿼터니언 변환 함수는 다음과 같다.
$$ \begin{align} Q_z(\psi) = \{cos(\frac{\psi}{2}), 0, 0, sin(\frac{\psi}{2}) \} \\ Q_y(\theta) = \{ cos(\frac{\theta}{2}), 0, sin(\frac{\theta}{2}), 0 \} \\ Q_x(\phi) = \{ cos(\frac{\phi}{2}), sin(\frac{\phi}{2}), 0, 0 \}\end{align}$$
서론에서 이야기했듯, 로봇 제어나 물리 시뮬레이션 등에서 쿼터니언은 많은 장점을 가지고 있다.
로봇이나 신체 분절의 orientation을 측정하기 위해 사용되는 IMU를 사용할 때에도 각 측정 값을 쿼터니언으로 변환하기 위해서 다양한 신호처리 기법이 사용된다. 나중에 기회가 되면 quaternion을 뽑아내는 것을 포함하여 다양한 방법의 IMU 신호처리에 대해서도 정리할 수 있을 것이다.
'Robotics > Geometry' 카테고리의 다른 글
| [Coordinate] Exponential Coordinates (0) | 2024.07.23 |
|---|---|
| [Rigid Body Motions] Body Twist (0) | 2024.07.19 |
| [Rigid Body Motions] Linear & Angular Velocities (0) | 2024.07.16 |
| [Transformation Matrices] Homogeneous Transformation (2) | 2023.10.15 |
| [Coordinate] 오일러 각 (Euler Angle) (1) | 2023.10.06 |