lastnamesong
[C++] 그리디 관련 문제 (백준 1931번, 회의실 배정) 본문
그리디 알고리즘 (Greedy Algorithm)
프로그래밍에서 어떤 선택이 “지금 가장 좋아 보이는 것”이라고 해서 최선의 해가 되는 것은 아니다. 하지만, 그런 탐욕스러운 선택이 오히려 정답으로 이어지는 경우가 있다. 이러한 전략을
lastnamesong.tistory.com
이전 글에서도 얘기는 했지만 그리디 알고리즘을 이해하는 것의 종착지는 "이 문제를 그리디로 풀 수 있는가?"를 판단하는 능력인 것 같다.
그리디 관련 문제 중 하나로 백준 온라인 저지의 1931번 "회의실 배정" 문제를 풀이해본다.
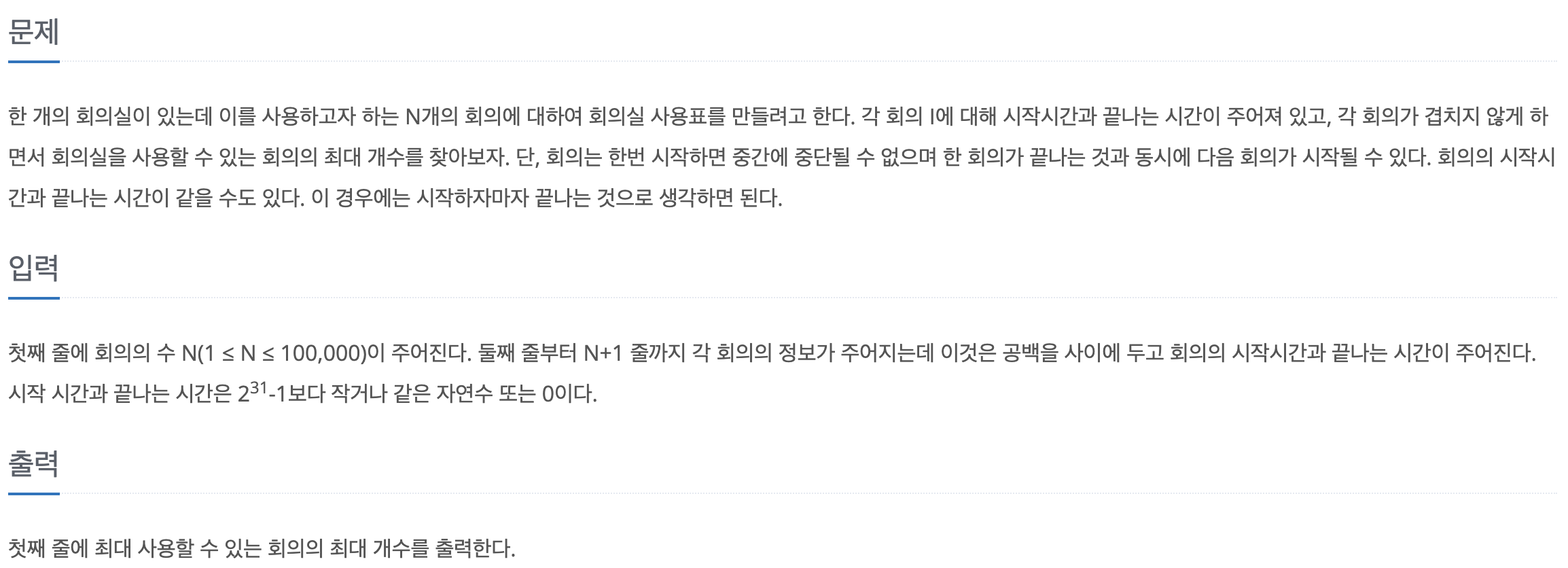
문제 분석 및 해결 전략
회의가 겹치지 않게 최대한 많은 회의를 진행해야 한다. 이는 완전탐색으로 해결하는 것보다는 주어진 회의 리스트에서 최적의 선택을 반복하는 그리디 알고리즘을 고려하는 것이 적절하다. 그 때 최적의 선택에 대한 기준이 필요할 것이다. 핵심은 회의를 시작시간이 아닌, 끝나는 시간 기준으로 정렬하는 것이다. 또한 종료 시간이 같으면 일찍 시작하는 회의가 앞에 오도록 정렬한다.
회의가 빨리 끝나면 그만큼 다음 회의를 빨리 시작할 수 있기 때문에 이런 규칙을 가지고 회의를 선택하다보면 최적의 답에 도달하는 것이다.
백준의 예제 입력을 손으로 풀어보면 더 쉽게 이해할 수 있다. (이미 끝나는 시간 순으로 정렬되어 있긴 하지만) 예제 입력에서 회의 정보와 관련된 정보를 정의한 기준에 맞게 그림으로 표현하면 아래와 같다.

정렬한 예제에서 가장 위에 있는 회의부터 시작하여 겹치지 않도록 선택을 하다보면, (1, 4), (5, 7), (8, 11), (12, 14) 네 개의 회의를 선택할 수 있다. 물론 맨 첫 번째 회의가 (1, 4)가 아니라 (3, 5)가 될 수도 있지만 정답에 영향을 주지는 않았다. 따라서 이 알고리즘을 코드로 구현할 수 있다면 문제를 풀 수 있을 것이다.
구현
C++에서 정렬할 때 sort함수에서 정렬하는 기준을 정의하여 위에서 정한 규칙대로 정렬할 수 있었다.
그리고 시간이 겹치지 않도록 endTime을 업데이트 하면서 회의 수를 늘려 나가는 식이다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
int N;
cin >> N;
vector<pair<int, int>> meetings(N);
for (int i = 0; i < N; i++) {
cin >> meetings[i].first >> meetings[i].second;
}
// 끝나는 시간이 빠른 순서로 정렬 (끝나는 시간이 같을 때에는 시작 시간이 빠른 순서로 정렬)
sort(meetings.begin(), meetings.end(), [](pair<int, int> a, pair<int, int> b) {
if (a.second == b.second) return a.first < b.first;
return a.second < b.second;
});
int count = 0;
int endTime = 0;
// 정렬된 순서대로 회의가 겹치지 않도록 각각을 확인
for (int i = 0; i < N; i++) {
if (meetings[i].first >= endTime) {
endTime = meetings[i].second;
count++;
}
}
cout << count << '\n';
return 0;
}검토하는 회의의 시작 시간이 확정된 가장 마지막 회의가 끝나는 시간보다 늦거나 같아야 하며 이를 조건문으로 구현했다.
그리디 알고리즘의 대표적인 적용 예제인 회의실 배정 문제를 풀어보았다. 핵심은 '끝나는 시간이 빠른 회의를 먼저 선택하는 것이 전체 회의 수를 최대로 늘릴 수 있는 전략'이라는 점이다. 이를 정렬과 순차 탐색으로 구현하면서, 그리디 알고리즘이 갖춰야 할 조건인 탐욕 선택 속성과 최적 부분 구조가 잘 드러나는 문제다.
실제로 코딩테스트에서는 이런 유형의 문제가 다양한 형태로 출제될 것이다. 면접 시간 예약, 강의실 스케줄, 기계 사용 시간 관리 등 실제 업무에서도 유사한 로직이 활용될 수도 있을 것 같다. 코딩 테스트를 비롯한 여러 실전의 문제들에 대해서 알고리즘적인 사고를 할 수 있는 사람이 참 대단하다는 것을 느낀다.
'Algorithm' 카테고리의 다른 글
| [C++] 정렬 함수 사용법 (sort 함수, 정렬 기준 다양하게) (0) | 2025.04.28 |
|---|---|
| 그리디 알고리즘 (Greedy Algorithm) (0) | 2025.04.21 |
| [C++] DFS 관련 문제 (백준 10451번, 순열 사이클) (0) | 2025.04.10 |
| [C++] '0'을 숫자 0으로 바꾸는 방법 (자료형, char, int) (0) | 2025.04.08 |
| [C++] BFS 관련 문제 (백준 2206번, 벽 부수고 이동하기) (0) | 2025.04.07 |





